Let P(h,k) be the point that satisfies the given property. We first consider the perpendicular lines. Two most simple perpendicular lines are
$y=0$ (that is, $x$-axis) and $x=0$ ($y$-axis).
Recall that the distance between a point $(h,k)$ and a line $ax+by+c=0$ is given by
$$ D = \left|\dfrac{ah+bk+c}{\sqrt{a^2+b^2}}\right|$$
Now the distance between the point $P$ and $x$-axis is $|k|$.
The distance between the point $P$ and $y$-axis is $|h|$.
It is given the sum of the above two distances is one. That means,
$$|h|+|k|=1$$
Note that the above equation is a set of four equations, which are
- $h+k=1$, when $P(h,k)$ lies on the first quadrant.
- $-h+k=1$, when $P(h,k)$ lies on the second quadrant.
- $-h-k=1$, when $P(h,k)$ lies on the third quadrant.
- $h-k=1$, when $P(h,k)$ lies on the fourth quadrant.
Note that above four equation represents together a square with corners at $(\pm1,0)$, $(0,\pm 1)$.
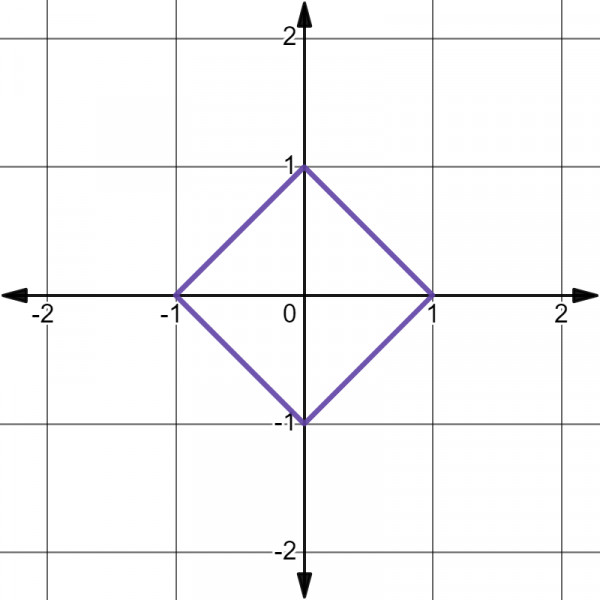
The correct answer is $A$.